d라이브러리

스피로그래프는 기하학적 그림을 그리는 장난감으로, 탐구하다 보면 수학적인 원리를 발견할 수 있습니다. 원의 회전으로 만들어지는 곡선의 종류인 트로코이드, 톱니 수와 관련된 최소공배수 등 다양한 수학 개념을 찾을 수 있는 스피로그래프에 대해 알아봅시다.

원을 회전시켜 만드는 곡선 ‘트로코이드’

스피로그래프는 다양한 종류의 트로코이드(trochoid) 곡선을 그리는 도구입니다. 1965년 영국의 공학자 데니스 피셔가 장난감으로 개발한 뒤 알려지기 시작했습니다. 스피로그래프는 크기가 서로 다른 두 개의 플라스틱 고리로 구성돼 있습니다. 그리고 큰 원 모양의 고리 내부와 작은 원 모양의 고리 외부에 톱니가 있습니다. 내부에 톱니가 있는 큰 원을 고정하고, 외부에 톱니가 있는 작은 원의 구멍에 필기구를 넣고 톱니끼리 맞닿게 돌리면 곡선을 그릴 수 있습니다.

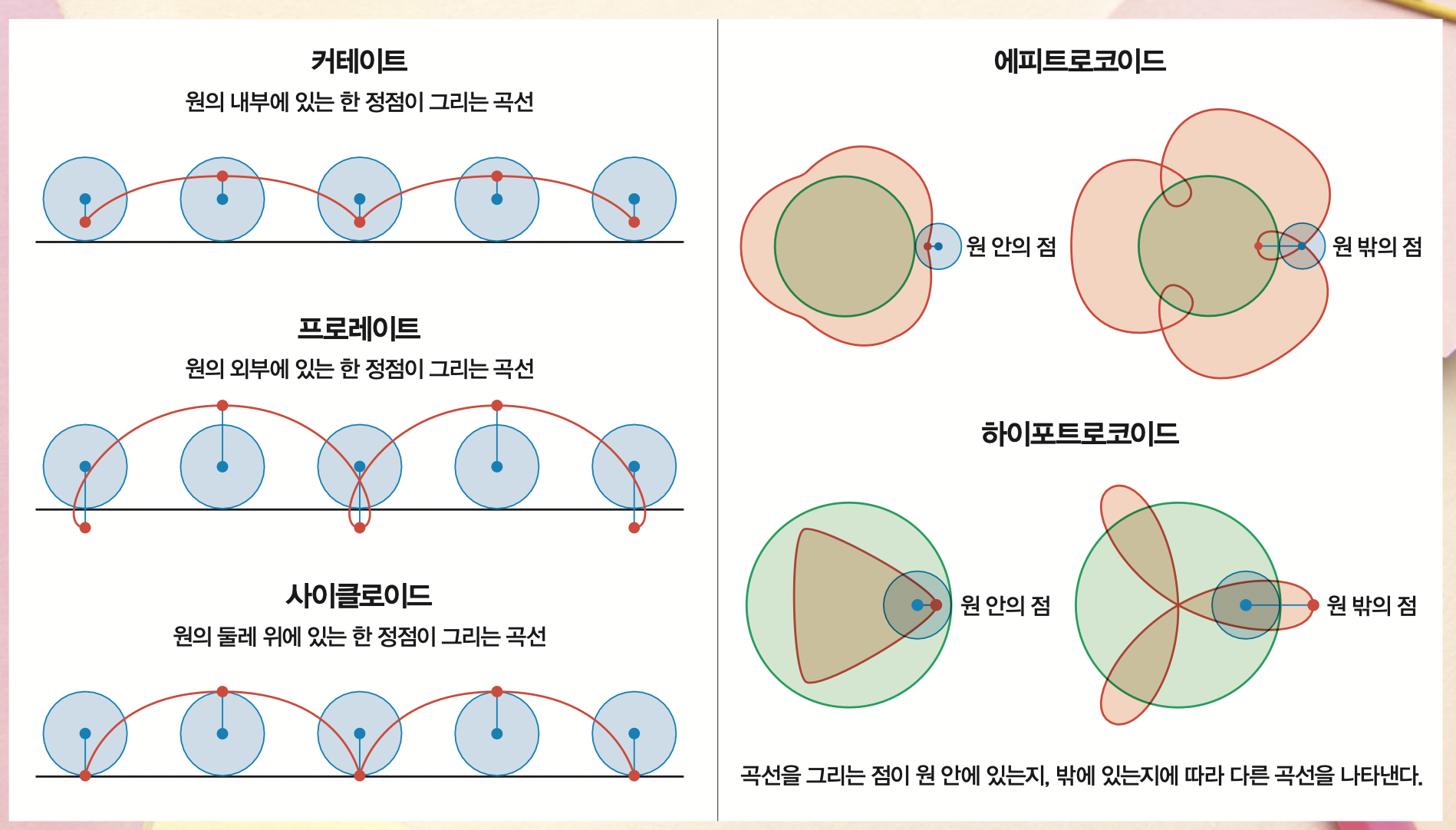
이때 그려지는 곡선은 원을 회전시키면 나오는 트로코이드 곡선입니다. 트로코이드는 선을 따라 굴러가는 원의 안 또는 바깥에 있는 한 정점이 그리는 곡선입니다. 또 원의 내부에 정점이 있을 때는 커테이트(curtate), 원의 외부에 정점이 있을 때는 프로레이트(prolate) 곡선이 그려집니다. 원의 둘레 위에 정점이 있을 때 그려지는 곡선은 사이클로이드(cycloid)라 합니다.

스피로그래프의 경우 톱니는 직선이 아닌 원 위를 따라 굴러갑니다. 따라서 이때는 원둘레를 따라 굴러갈 때 생기는 트로코이드인 에피트로코이드와 하이포트로코이드를 만듭니다. 에피트로코이드는 외부라는 뜻의 ‘에피(epi)’와 트로코이드가 합쳐진 단어로, 원 바깥에 다른 원이 굴러갈 때 회전 원의 내부, 외부, 둘레에 있는 점이 그리는 곡선을 뜻합니다. 반대로 작은 원이 원의 안쪽을 굴러갈 때는 내부라는 뜻의 ‘하이포(hypo)’와 트로코이드가 합쳐진 하이포트로코이드 곡선을 그립니다.

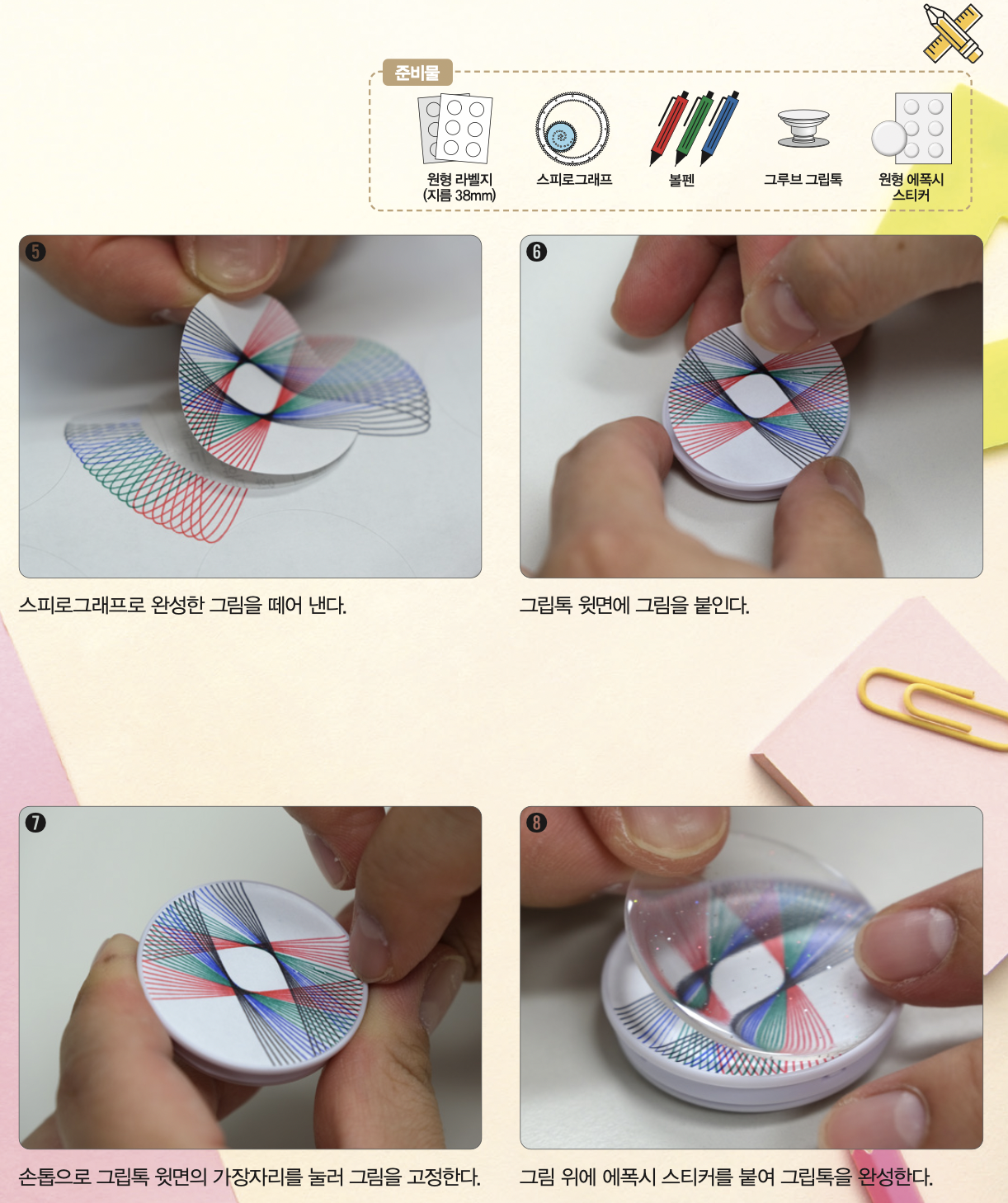
큰 원 모양의 톱니 안 또는 밖에 작은 원 톱니가 돌아가는 스피로그래프를 이용해 에피트로코이드나 하이포트로코이드 곡선을 그릴 수 있습니다. 이를 이용해 그립톡을 만들어봅시다.